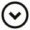- p and q will be given to you.
| Number: pq | |
| p | q |
| 120 | 650 |
| 12561 | 345 |
| 122 | 556 |
| 243 | 329 |
| 124 | 7777 |
| 1245 | 89782 |
| 1246 | 234 |
| 1247 | 124 |
| 1248 | 25 |
| 1249 | 45 |
45/2=22
45%2=1
| Unit digit(m) | Unit digit produced from power(n) of m (mn) | Formula For unit digit calculation | p | q | Unit digits of pq |
| 0 | 0 | 0 | 120 | 650 | 0 |
| 1 | 1 | 1 | 12561 | 345 | 1 |
| 2 | 2, 4 , 8, 6 | (n%4)th digit of the sequence | 122 | 556 | 6 |
| 3 | 3, 9, 7, 1 | (n%4)th digit of the sequence | 243 | 3 | 7 |
| 4 | 4, 6 | (n%2)th digit of the sequence | 124 | 7777 | 4 |
| 5 | 5 | 5 | 1245 | 89782 | 5 |
| 6 | 6 | 6 | 1246 | 234 | 6 |
| 7 | 7, 9, 3, 1 | (n%4)th digit of the sequence | 1247 | 124 | 1 |
| 8 | 8, 4, 2, 6 | (n%4)th digit of the sequence | 1248 | 25 | 8 |
| 9 | 9, 1 | (n%2)th digit of the sequence | 1249 | 45 | 9 |
Important Note: if n%4 or n%2 provides result 0, the last digit of the sequence will be the unit digit of mn
For details, see the video https://youtu.be/b6lbcfMcaF4